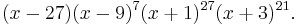Gosset graph
| Gosset graph | |
|---|---|
Gosset graph (321) (Two vertices coincide in the center of this graph. Edges also coincide with this projection.) |
|
| Named after | Thorold Gosset |
| Vertices | 56 |
| Edges | 756 |
| Radius | 3 |
| Diameter | 3 |
| Girth | 3 |
| Automorphisms | 2903040 |
| Properties | Distance-regular graph Integral Vertex-transitive |
The Gosset graph, named after Thorold Gosset, is a specific regular graph (1-skeleton of the 7-dimensional 321 polytope) with 56 vertices and valency 27.
Construction
The Gosset graph can be explicitly constructed as follows: the 56 vertices are the vectors in R8, obtained by permuting the coordinates and possibly taking the opposite of the vector (3, 3, −1, −1, −1, −1, −1, −1). Two such vectors are adjacent when their inner product is 8.
Properties
In the above representation, two vertices are at distance two when ther inner product is −8 and at distance three when their inner product is −24 (which is only possible if the vectors are each other's opposite). The Gosset graph is distance-regular with diameter three.
The automorphism group of the Gosset graph is isomorphic to the Coxeter group E7 and hence has order 2903040. The Gosset 321 polytope is a semiregular polytope. Therefore the automorphism group of the Gosset graph, E7, acts transitively upon its vertices, making it a vertex-transitive graph.
The characteristic polynomial of the Gosset graph is
Therefore this graph is an integral graph.
References
- Weisstein, Eric W., "Gosset Graph" from MathWorld.